18 Missing values
18.1 Introduction
你已经在前面的章节中学习了缺失值的基础知识。 首次接触是在 Chapter 1 中，它们在绘图时引发了警告；在 Section 3.5.2 中，它们干扰了汇总统计量的计算；你还了解了它们的传染性特性，并在 Section 12.2.2 中学习了如何检查它们的存在。 现在我们将更深入地探讨缺失值，以便你了解更多细节。
我们将首先讨论处理以 NAs 形式记录的缺失值的一些通用工具。 接着探讨隐式缺失值的概念——即数据中直接不存在的值——并展示一些可将其显式化的工具。 最后我们将讨论由数据中未出现的因子水平引起的空组相关问题。
18.1.1 Prerequisites
处理缺失数据的函数主要来自 dplyr 和 tidyr，它们是 tidyverse 的核心包。
18.2 Explicit missing values
首先，我们来探索几个便捷工具，用于创建或消除显式缺失值（即单元格中显示为 NA 的情况）。
18.2.1 Last observation carried forward
缺失值的一个常见用途是作为数据输入的便捷方式。 当数据是手动录入时，缺失值有时表示前一行的值已被重复（或前向填充）：
treatment <- tribble(
~person, ~treatment, ~response,
"Derrick Whitmore", 1, 7,
NA, 2, 10,
NA, 3, NA,
"Katherine Burke", 1, 4
)你可以使用 tidyr::fill() 来填充这些缺失值。 它的用法类似 select()，接收一组列名：
treatment |>
fill(everything())
#> # A tibble: 4 × 3
#> person treatment response
#> <chr> <dbl> <dbl>
#> 1 Derrick Whitmore 1 7
#> 2 Derrick Whitmore 2 10
#> 3 Derrick Whitmore 3 10
#> 4 Katherine Burke 1 4这种处理方式有时被称为“最后观测值前向填充”（last observation carried forward），简称 locf。 你可以使用 .direction 参数来填充以其他特殊方式生成的缺失值。
18.2.2 Fixed values
有时，缺失值代表某个固定且已知的值，最常见的是 0。 你可以使用 dplyr::coalesce() 来替换它们：
有时你会遇到相反的问题：某些具体值实际上代表缺失值。 这通常出现在由旧版软件生成的数据中，这些软件没有合适的方式来表示缺失值，因此必须使用像 99 或 -999 这样的特殊值来代替。
如果可能，应在读取数据时处理此问题，例如使用 readr::read_csv() 的 na 参数，如 read_csv(path, na = "99")。 如果之后才发现问题，或者数据源在读取时未提供处理方式，你可以使用 dplyr::na_if()：
18.2.3 NaN
在继续之前，有一种特殊类型的缺失值你偶尔会遇到：NaN（读作 “nan”），即非数字。 了解它并不那么重要，因为它通常表现得就像 NA:：
在极少数需要区分 NA 和 NaN 的情况下，你可以使用 is.nan(x)。
通常，当你执行具有不确定结果的数学运算时，会遇到 NaN：
0 / 0
#> [1] NaN
0 * Inf
#> [1] NaN
Inf - Inf
#> [1] NaN
sqrt(-1)
#> Warning in sqrt(-1): NaNs produced
#> [1] NaN18.3 Implicit missing values
到目前为止，我们讨论的都是显式缺失值，即你可以在数据中看到 NA。 但缺失值也可能是隐式缺失的，如果整行数据在数据集中直接不存在。 让我们通过一个记录某股票每季度价格的简单数据集来说明这种差异：
这个数据集有两个缺失的观测值：
2020 年第四季度的
price是显式缺失的，因为它的值是NA。2021 年第一季度的
price是隐式缺失的，因为它根本没有出现在数据集中。
理解这种差异的一种方式是借用禅宗公案式的比喻：
显式缺失值是“存在的缺席”。
隐式缺失值是“缺席的存在”。
有时，你希望将隐式缺失变为显式，以便进行实际操作。 而在其他情况下，数据的结构会强制产生显式缺失，你可能希望消除它们。 以下部分讨论一些在隐式与显式缺失之间转换的工具。
18.3.1 Pivoting
你已经见过一种能使隐式缺失显式化（反之亦然）的工具：pivoting。 将数据变宽可以使隐式缺失值显式化，因为每一行与新列的组合都必须有某个值。 例如，如果我们 pivot stocks 数据，将 quarter 放在列中，两个缺失值都会变为显式：
stocks |>
pivot_wider(
names_from = qtr,
values_from = price
)
#> # A tibble: 2 × 5
#> year `1` `2` `3` `4`
#> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 2020 1.88 0.59 0.35 NA
#> 2 2021 NA 0.92 0.17 2.66默认情况下，将数据变长会保留显式缺失值，但如果这些缺失值是因数据不整洁而产生的结构性缺失值，你可以通过设置 values_drop_na = TRUE 来删除它们（使其变为隐式）。 更多细节参见 Section 5.2 中的示例。
18.3.2 Complete
tidyr::complete() 允许你通过提供一组变量来生成显式缺失值，这些变量定义了应该存在的行组合。 例如，我们知道 year 和 qtr 的所有组合都应该存在于 stocks 数据中：
stocks |>
complete(year, qtr)
#> # A tibble: 8 × 3
#> year qtr price
#> <dbl> <dbl> <dbl>
#> 1 2020 1 1.88
#> 2 2020 2 0.59
#> 3 2020 3 0.35
#> 4 2020 4 NA
#> 5 2021 1 NA
#> 6 2021 2 0.92
#> # ℹ 2 more rows通常，你会用现有变量的名称调用 complete()，以填充缺失的组合。 然而，有时单个变量本身就不完整，因此你可以改为提供自己的数据。 例如，你可能知道 stocks 数据集应该涵盖 2019 到 2021 年，因此可以明确为 year 提供这些值：
stocks |>
complete(year = 2019:2021, qtr)
#> # A tibble: 12 × 3
#> year qtr price
#> <dbl> <dbl> <dbl>
#> 1 2019 1 NA
#> 2 2019 2 NA
#> 3 2019 3 NA
#> 4 2019 4 NA
#> 5 2020 1 1.88
#> 6 2020 2 0.59
#> # ℹ 6 more rows如果变量的范围是正确的，但并非所有值都存在，你可以使用 full_seq(x, 1) 来生成从 min(x) 到 max(x)、间隔为 1 的所有值。
在某些情况下，完整的观测集无法通过变量的简单组合生成。 这时，你可以手动执行 complete() 所做的事情：创建一个包含所有应该存在的行的数据框（使用你需要的任何技术组合），然后通过 dplyr::full_join() 将其与原始数据集合并。
18.3.3 Joins
这引出了揭示隐式缺失观测的另一种重要方法：joins。 你将在 Chapter 19 中更详细地学习连接操作，但这里我们想快速提及它们，因为通常只有通过与其他数据集比较，才能发现某个数据集中缺失的值。
dplyr::anti_join(x, y) 在这里是一个特别有用的工具，因为它只选择在 y 中没有匹配项的 x 中的行。 例如，我们可以使用两次 anti_join()s 来揭示 flights 数据中缺少四个机场和 722 架飞机的信息：
library(nycflights13)
flights |>
distinct(faa = dest) |>
anti_join(airports)
#> Joining with `by = join_by(faa)`
#> # A tibble: 4 × 1
#> faa
#> <chr>
#> 1 BQN
#> 2 SJU
#> 3 STT
#> 4 PSE
flights |>
distinct(tailnum) |>
anti_join(planes)
#> Joining with `by = join_by(tailnum)`
#> # A tibble: 722 × 1
#> tailnum
#> <chr>
#> 1 N3ALAA
#> 2 N3DUAA
#> 3 N542MQ
#> 4 N730MQ
#> 5 N9EAMQ
#> 6 N532UA
#> # ℹ 716 more rows18.3.4 Exercises
- 你能找到航空公司与
planes中似乎缺失的行之间的任何关系吗？
18.4 Factors and empty groups
最后一种缺失类型是空组，即不包含任何观测值的组，这在处理因子时可能出现。 例如，假设我们有一个包含人们健康信息的数据集：
我们想用 dplyr::count() 统计吸烟者数量：
health |> count(smoker)
#> # A tibble: 1 × 2
#> smoker n
#> <fct> <int>
#> 1 no 5该数据集中只包含非吸烟者，但我们知道吸烟者是存在的；非吸烟者组是空的。 我们可以要求 count() 保留所有组，即使数据中未出现的组，通过使用 .drop = FALSE：
health |> count(smoker, .drop = FALSE)
#> # A tibble: 2 × 2
#> smoker n
#> <fct> <int>
#> 1 yes 0
#> 2 no 5同样的原则适用于 ggplot2 的离散坐标轴，它们也会删除没有任何值的水平。 你可以通过向相应的离散坐标轴提供 drop = FALSE 来强制显示它们：
ggplot(health, aes(x = smoker)) +
geom_bar() +
scale_x_discrete()
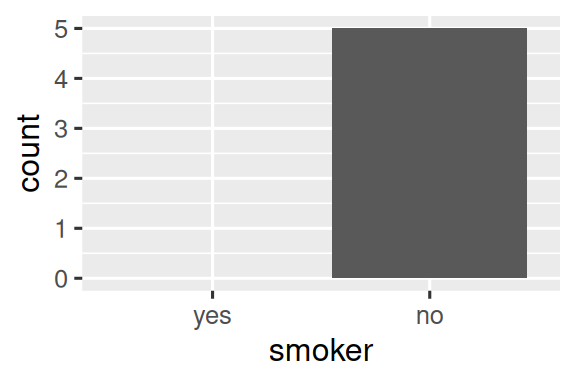
ggplot(health, aes(x = smoker)) +
geom_bar() +
scale_x_discrete(drop = FALSE)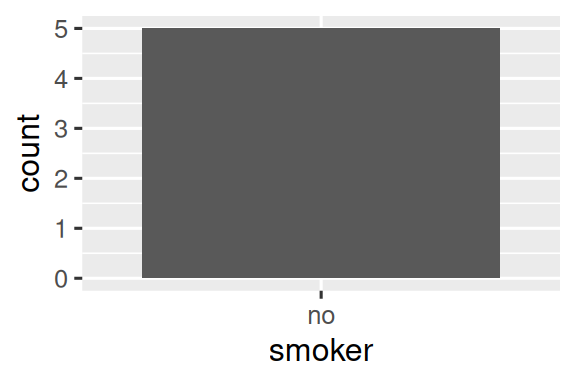
{fig-alt=’A bar chart with a single value on the x-axis, “no”.
The same bar chart as the last plot, but now with two values on the x-axis, “yes” and “no”. There is no bar for the “yes” category.’ width=288}
{fig-alt=’A bar chart with a single value on the x-axis, “no”.
The same bar chart as the last plot, but now with two values on the x-axis, “yes” and “no”. There is no bar for the “yes” category.’ width=288}
同样的问题在 dplyr::group_by() 中更普遍地出现。 同样，你可以使用 .drop = FALSE 来保留所有因子水平：
health |>
group_by(smoker, .drop = FALSE) |>
summarize(
n = n(),
mean_age = mean(age),
min_age = min(age),
max_age = max(age),
sd_age = sd(age)
)
#> # A tibble: 2 × 6
#> smoker n mean_age min_age max_age sd_age
#> <fct> <int> <dbl> <dbl> <dbl> <dbl>
#> 1 yes 0 NaN Inf -Inf NA
#> 2 no 5 60 34 88 21.6我们在这里得到一些有趣的结果，因为在汇总空组时，汇总函数会应用于长度为零的向量。 空向量（长度为0）与缺失值（每个长度为1）之间存在重要区别。
所有汇总函数都能处理长度为零的向量，但它们返回的结果可能初看令人惊讶。 这里我们看到 mean(age) 返回 NaN，因为 mean(age) = sum(age)/length(age)，而此处为 0/0。 max() 和 min() 对空向量返回 -Inf 和 Inf，因此如果将这些结果与新的非空数据向量合并并重新计算，你会得到新数据的最小值或最大值1。
有时，更简单的方法是先执行汇总，然后用 complete() 将隐式缺失值显式化。
health |>
group_by(smoker) |>
summarize(
n = n(),
mean_age = mean(age),
min_age = min(age),
max_age = max(age),
sd_age = sd(age)
) |>
complete(smoker)
#> # A tibble: 2 × 6
#> smoker n mean_age min_age max_age sd_age
#> <fct> <int> <dbl> <dbl> <dbl> <dbl>
#> 1 yes NA NA NA NA NA
#> 2 no 5 60 34 88 21.6这种方法的主要缺点是，即使你知道计数应为零，却得到了一个 NA。
18.5 Summary
缺失值真奇怪！ 有时它们被记录为显式的 NA，但其他时候你只能通过它们的缺失来察觉。 本章为你提供了一些处理显式缺失值的工具、揭示隐式缺失值的工具，并讨论了隐式缺失值如何变为显式以及相反情况的一些方式。
在下一章，我们将讨论本书这一部分的最后一章：连接。 这与之前的章节略有不同，因为我们将讨论处理整个数据框的工具，而不是放入数据框内部的工具。
也就是说，
min(c(x, y))总是等于min(min(x), min(y))。↩︎